Binary Tree (이진 트리)
루트 노드를 중심으로 두 개의 서브 트리로 나눠진다. 또한 나눠진 두 서브 크리도 모두 이진 트리여야한다.
트리에서는 각 층별로 숫자를 매겨 이를 트리의 level이라고 한다.
레벨의 값은 0부터 시작하고 따라서 루트 노드의 레벨은 0이다.
그리고 트리의 최고 레벨을 가리켜 해당 트리의 height라고 한다.
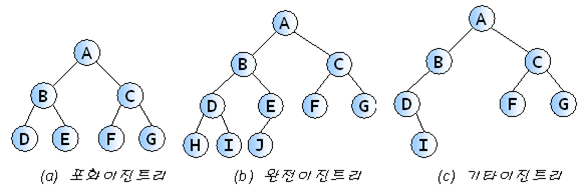
Perfect Binary Tree (포화 이진 트리)
모든 레벨이 꽉 차있고 각 레벨이 허용하는 최대 자식 노드 개수를 가지고 있는 트리를 말합니다.
Complete Binary Tree (완전 이진 트리)
부모, 왼쪽 자식, 오른쪽 자식 순으로, 꽉 채워지며 만들어지는 이진 트리 또는, 포화 이진 트리의 맨아래 단말 노드들을 오른쪽부터 하나씩 제거하여 얻어지는 트리
BST (Binary Search Tree)
이진 탐색 트리는 이진 트리의 일종이다. 단 이진 탐색 트리에는 데이터를 저장하는 규칙이 있고 그 규칙을 통해 특정 데이터의 위치를 찾는데 사용할 수 있다.
- 규칙 1. 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 규칙 2. 부모의 키가 왼쪽 자식 노드의 키보다 크다.
- 규칙 3. 부모의 키가 오른쪽 자식 노드의 키보다 작다.
- 규칙 4. 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
이진 탐색 트리의 탐색 연산은 O(log n)의 시간 복잡도를 갖는다.
하지만 이러한 이진 탐색 트리는 Skewed Tree(편향 트리)가 될 수 있다.
저장 순서에 따라 계속 한 쪽으로만 노드가 추가되는 경우가 발생하기 때문이다.
이럴 경우 성능에 영향을 미치게 되며, 탐색의 Worst Case 가 되고 **시간 복잡도는 O(n)**이 된다.
Binary Heap
자료구조의 일종으로 Tree의 형식을 하고 있으며 Tree중에서도 배열에 기반한 Complete Binary Tree이다.
힙(Heap)에는 최대힙(max heap), 최소힙(min heap) 두 종류가 있다.
Max Heap이란, 각 노드의 값이 해당 children 의 값보다 크거나 같은 complete binary tree를 말한다. ( Min Heap 은 그 반대이다.) 루트 노드가 최대값이기 때문에 최대값을 찾는데 소요되는 연산의 시간 복잡도는 O(1)이다.
삽입
새 data를 마지막 Node에 삽입합니다. 그 다음 부모 노드와 비교해 가면서 부모 노드가 더 작다면 swap을 해줍니다.


삭제
삭제는 항상 루트 노드를 삭제를 합니다.

제거가 된 후에 가장 마지막 Node가 루트노드로 이동을 한다.

최대힙 조건을 갖춰야 하므로 계속해서 자식 Node 와 비교를 해가면서 필요시 Swap을 합니다.
현재 루트노드의 값은 아래 두 자식노드보다 작습니다.
이 경우 두 자식노드 모두 루트노드와 Swap이 가능합니다.
이러한 경우엔 최대힙인 경우는 두 자식노드중 더 큰 값을 가지는 노드가, 최소힙인 경우는 두 자식노드중 더 작은 값을 가지는 노드가 부모노드와 Swap이 이루어집니다.
'기술 면접 정리' 카테고리의 다른 글
| 알고리즘 이론 깨부수기 Hash Table (0) | 2022.06.04 |
|---|---|
| 알고리즘 이론 깨부수기 그래프 (0) | 2022.06.03 |
| Socket.io와 Webksocket의 차이 (0) | 2022.05.16 |
| react vs next.js vs svelte (0) | 2022.05.08 |
| WebSocket 프로토콜 (0) | 2022.05.01 |