Stack
선형 자료구조의 일종으로 Last In First Out (LIFO). 즉, 나중에 들어간 원소가 먼저 나온다. 이것은 Stack 의 가장 큰 특징이다. 차곡차곡 쌓이는 구조로 먼저 Stack 에 들어가게 된 원소는 맨 바닥에 깔리게 된다. 그렇기 때문에 늦게 들어간 녀석들은 그 위에 쌓이게 되고 호출 시 가장 위에 있는 녀석이 호출되는 구조이다.
스택 추상 자료형
객체: 후입선출(LIFO)의 접근 방법을 유지하는 요소들의 모음
push(x): 주어진 요소 x를 스택의 맨 위에 추가한다.
pop(): 스택이 비어있지 않으면 맨 위에 있는 요소를 삭제하고 반환한다.
isEmpty(): 스택이 비어있으면 참(true)을 아니면 거짓(false)을 반환한다.
peek(): 스택이 비어있지 않으면 맨 위에 있는 요소를 삭제하지 않고 반환한다.
isFull(): 스택이 가득 차 있으면 참(true)을 아니면 거짓(false)을 반환한다
size(): 스택내의 모든 요소들의 개수를 반환한다.
display(): 스택내의 모든 요소들의 출력한다.
배열을 이용한 스택의 구현
1차원 배열을 기반으로 한 스택
- top: 가장 최근에 입력되었던 자료를 가리키는 변수
- data[0] … data[top]: 먼저 들어온 순으로 저장
- 공백상태이면 top은 -1
- 포화상태이면 top은 MAX_STACK_SIZE - 1

Stack에 실사용 예제
컴퓨터에서 자료구조 Stack은 어떤 곳에 사용되고 있을까요? 대표적으로 우리가 자주 사용하는 브라우저의 뒤로 가기, 앞으로 가기 기능을 구현할 때 자료구조 Stack이 활용됩니다.
Queue
선형 자료구조의 일종으로 First In First Out (FIFO). 즉, 먼저 들어간 놈이 먼저 나온다. Stack 과는 반대로 먼저 들어간 놈이 맨 앞에서 대기하고 있다가 먼저 나오게 되는 구조이다.
객체: 선입선출(FIFO)의 접근 방법을 유지하는 요소들의 모음
연산:
▪ enqueue(e): 주어진 요소 e를 큐의 맨 뒤에 추가한다.
▪ dequeue(): 큐가 비어있지 않으면 맨 앞 요소를 삭제하고 반환한다.
▪ peek(): 큐가 비어있지 않으면 맨 앞 요소를 삭제하지 않고 반환한다.
▪ isEmpty(): 큐가 비어있으면 true를 아니면 false를 반환한다.
▪ isFull(): 큐가 가득 차 있으면 true을 아니면 false을 반환한다.
▪ size(): 큐의 모든 요소들의 개수를 반환한다.
▪ display(): 큐의 모든 요소들의 출력한다.
배열을 이용한 큐: 선형큐
- 배열을 선형으로 사용하여 큐를 구현
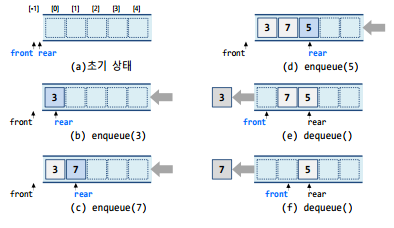
- 문제점: 삽입을 계속하기 위해서는 요소들을 이동시켜야함
원형큐
원형큐의 구조
전단과 후단을 관리하기 위한 2개의 변수 필요
front: 첫번째 요소 하나 앞의 인덱스
rear: 마지막 요소의 인덱스
삽입과 삭제연산
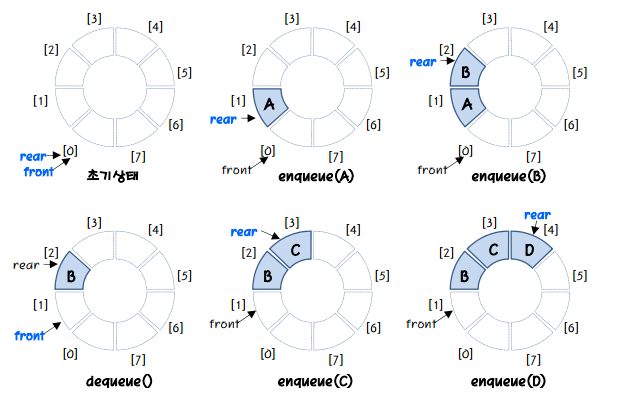
- 공백상태: front == rear
- 포화상태: front == (rear+1) % M
- 공백상태와 포화상태를 구별 방법은?
- 하나의 공간은 항상 비워 두는 이유? front와 rear가 같기 때문에 비어있는 경우와 혼동할 수 있다.

Queue의 실사용 예제
자료구조 Queue는 컴퓨터에서도 광범위하게 활용됩니다. 컴퓨터와 연결된 프린터에서 여러 문서를 순서대로 인쇄하려면 어떻게 해야 할까요?
- 우리가 문서를 작성하고 출력 버튼을 누르면 해당 문서는 인쇄 작업 (임시 기억 장치의) Queue에 들어갑니다.
- 프린터는 인쇄 작업 Queue에 들어온 문서를 순서대로 인쇄합니다.
데이터(data)를 주고 받을 때, 각 장치 사이에 존재하는 속도의 차이나 시간 차이를 극복하기 위해 임시 기억 장치의 자료구조로 Queue를 사용합니다.
Tree
트리는 스택이나 큐와 같은 선형 구조가 아닌 비선형 자료구조이다. 트리는 계층적 관계(Hierarchical Relationship)을 표현하는 자료구조이다. 이 트리라는 자료구조는 표현에 집중한다.
트리를 구성하고 있는 구성요소들(용어)
- Node (노드) : 트리를 구성하고 있는 각각의 요소를 의미
- Edge (간선) : 트리를 구성하기 위해 노드와 노드를 연결하는 선을 의미
- Root Node (루트 노드) : 트리 구조에서 최상위에 있는 노드를 의미
- Terminal Node ( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드를 의미
- Internal Node (내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함
Binary Tree (이진 트리)

루트 노드를 중심으로 두 개의 서브 트리(큰 트리에 속하는 작은 트리)로 나뉘어 진다. 또한 나뉘어진 두 서브 트리도 모두 이진 트리어야 한다. 재귀적인 정의라 맞는듯 하면서도 이해가 쉽지 않을 듯하다. 한 가지 덧붙이자면 공집합도 이진 트리로 포함시켜야 한다. 그래야 재귀적으로 조건을 확인해갔을 때, leaf node 에 다다랐을 때, 정의가 만족되기 때문이다. 자연스럽게 노드가 하나 뿐인 것도 이진 트리 정의에 만족하게 된다.
BST (Binary Search Tree)
효율적인 탐색을 위해서는 어떻게 찾을까만 고민해서는 안된다. 그보다는 효율적인 탐색을 위한 저장방법이 무엇일까를 고민해야 한다. 단 이진 탐색 트리에는 데이터를 저장하는 규칙이 있다. 그리고 그 규칙은 특정 데이터의 위치를 찾는데 사용할 수 있다.
- 규칙 1. 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 규칙 2. 부모의 키가 왼쪽 자식 노드의 키보다 크다.
- 규칙 3. 부모의 키가 오른쪽 자식 노드의 키보다 작다.
- 규칙 4. 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.

특징(Properties) :
☞ 좌측 하위 트리(Left Subtree)의 노드들은 상위 노드보다 작거나 같은 값입니다.
☞ 우측 하위 트리(Right Subtree)의 노드들은 상위 노드보다 큰 값입니다.
☞ 좌측 및 우측 하위트리 역시 이진 탐색 트리입니다. (하위트리의 하위트리들도 모두 위 특징에 해당합니다)
탐색(Search) :
☞ 탐색의 시작은 루트 노드(Root Node)에서 시작합니다. 만약 탐색하려는 값이 루트 노드의 값이라면 루트 노드의 값을 반환합니다.
☞ 만약 탐색하려는 값이 루트 노드의 값보다 작다면 좌측 하위 트리로 이동해서 탐색을 반복합니다.
☞ 만약 탐색하려는 값이 루트 노드의 값보다 크다면 우측 하위 트리로 이동해서 탐색을 반복합니다.
이진 탐색 트리의 탐색 연산은 O(log n)의 시간 복잡도를 갖는다. 이러한 이진 탐색 트리는 Skewed Tree(편향 트리)가 될 수 있다. 저장 순서에 따라 계속 한 쪽으로만 노드가 추가되는 경우가 발생하기 때문이다. 이럴 경우 성능에 영향을 미치게 되며, 탐색의 Worst Case 가 되고 시간 복잡도는 O(n)이 된다.